4.3. Оценка качества функциональной схемы
Задача оценки качества функциональной схемы является
нетривиальной, так как необходимо наиболее полно отразить
окончательные показатели качества той реальной электрической
схемы, которая будет изготовлена на основе функциональной, и в
то же время, выполнить эту оценку полагаясь на информацию,
которую несет в себе функциональная схема.
Возникающее противоречие связано с тем, что на качество
электрической схемы (блока) сильное влияние окажут конструкторские
параметры - размеры и расположение печатных плат, вид монтажа,
способ трассировки связей и другие, не известные еще на этапе
логического проектирования. Поэтому целесообразно поставить
задачу приближенной оценки качества функциональной схемы,
решение которой позволило бы отобрать некоторое ограниченное
множество равноценных по качеству функциональных схем, пригодных
для дальнейшей детальной проработки. Наиболее простым является
способ оценки функциональной схемы по двум параметрам: задержке
распространения T и аппаратурным затратам M. При этом необходимо
определиться с типом элементной базы (типом и серией ИС), который
чаще всего задается уже на этапе эскизного проектирования.
Задержку логической схемы можно приближенно оценить значением
среднего времени задержки распространения tзд.р.ср. входящих в
нее алгоритмов. Как правило, для данной логической серии можно
считать tзд.р. одинаковым для простых функциональных элементов
(И-НЕ, И, ИЛИ, НЕ) и свести его к усредненной величине
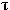 . .
Задержки вносимые более сложными ИС рекомендуется округлить
до кратных 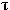 или или 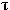 /2. /2.
Аппаратурные затраты можно оценить различными способами:
- по площади, занимаемой корпусом ИС на печатной плате;
- по соотношению площадей корпусов к числу выводов;
- суммарным числом выводов всех используемых корпусов.
Для примера используем схему, рассмотренную в разделе 4.2.
Для функциональной схемы рис. 4.4.
(базис 2ИЛИ-НЕ) имеем: Т = 9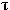 , M,
выраженное в числе корпусов получится равным 34/4 = 8 + 1/2 , M,
выраженное в числе корпусов получится равным 34/4 = 8 + 1/2
Для функциональной cхемы рис. 4.3.
(базис 2И-НЕ) имеем: Т=10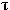 , M = 8 + 3/4 , M = 8 + 3/4
Для функциональной cхемы рис. 4.5.
(базис 2И, 2ИЛИ, НЕ): Т=8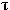 ,
M = 5/6 + 17/4 + 6/4 = 5/6 + 23/4 = (20 + 6 * 23)/24 =
(10 + 3 * 23)/12 = (10 + 69)/12 = 79/12 = 6 + 7/12 ,
M = 5/6 + 17/4 + 6/4 = 5/6 + 23/4 = (20 + 6 * 23)/24 =
(10 + 3 * 23)/12 = (10 + 69)/12 = 79/12 = 6 + 7/12
Мы видим, что число корпусов и величина задержки достаточно
велики даже для универсального базиса. Попробуем определить
функциональный набор наиболее оптимальный для данной схемы.
Используя функциональные элементы 3И, 3ИЛИ, 2И-НЕ, НЕ можно
получить схему (рис. ). Получается выигрыш по задержке по сравнению
со схемой (2И, 2ИЛИ, НЕ), но некоторый проигрыш по числу корпусов.
Легко заметить также, что использование в качестве инверторов
элементов Шеффера (2И-НЕ) нерационально и следует попытаться
использовать непосредственно элементы 3И. Тогда получим следующую
схему (рис. 4.6.). Параметры этой схемы оказываются самыми
оптимальными.
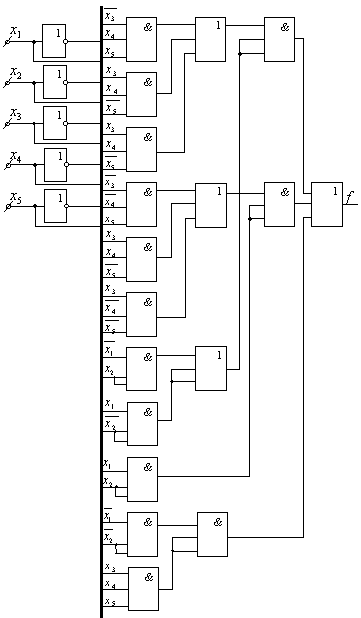
Рис. 4.6.
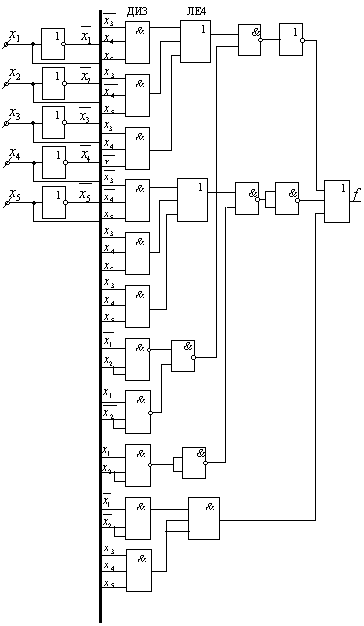
Рис. 4.7.
|

