.gif) |
4.2. Приведение булевых функций к данному функциональному базису
и построение функциональной схемы
Для получения функциональной схемы, соответствующей заданной
функции алгебры логики, необходимо выразить эту функцию в
некотором функционально полном базисе и сопоставить каждой
элементарной функции функциональный элемент ей соответствующий.
Процесс такого преобразования состоит в последовательной декомпозиции
исходной формы представления заданной функции на подфункции,
представленные в заданном функциональном базисе и продолжается
до тех пор, пока не будет найдена эквивалентная БФ в требуемом
базисе.
Исследуем это преобразование с помощью следующего содержательного
примера.
Предположим, что в некотором декодирующем устройстве требуется
распознавать кодовые комбинации по их весу (для двоичного кода
вес КК равен числу единиц, имеющихся в этой КК). Будем считать,
что одна из КС должна формировать на выходе логическую "1", если
на ее входах имеется КК с весом равным 3. Обобщенная структура
такой схемы представлена на рис. 4.2
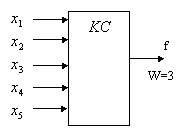
Рис. 4.2.
Таблица истинности требуемой БФ получит вид:
Таблица 4.1. Истинности требуемой БФ
| № вх.набора |
X1 |
X2 |
X3 |
X4 |
X5 |
f |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
1 |
0 |
| 2 |
0 |
0 |
0 |
1 |
0 |
0 |
| 3 |
0 |
0 |
0 |
1 |
1 |
0 |
| 4 |
0 |
0 |
1 |
0 |
0 |
0 |
| 5 |
0 |
0 |
1 |
0 |
1 |
0 |
| 6 |
0 |
0 |
1 |
1 |
0 |
0 |
| 7 |
0 |
0 |
1 |
1 |
1 |
1 |
| 8 |
0 |
1 |
0 |
0 |
0 |
0 |
| 9 |
0 |
1 |
0 |
0 |
1 |
0 |
| 10 |
0 |
1 |
0 |
1 |
0 |
0 |
| 11 |
0 |
1 |
0 |
1 |
1 |
1 |
| 12 |
0 |
1 |
1 |
0 |
0 |
0 |
| 13 |
0 |
1 |
1 |
0 |
1 |
1 |
| 14 |
0 |
1 |
1 |
1 |
0 |
1 |
| 15 |
0 |
1 |
1 |
1 |
1 |
0 |
| 16 |
1 |
0 |
0 |
0 |
0 |
0 |
| 17 |
1 |
0 |
0 |
0 |
1 |
0 |
| 18 |
1 |
0 |
0 |
1 |
0 |
0 |
| 19 |
1 |
0 |
0 |
1 |
1 |
1 |
| 20 |
1 |
0 |
1 |
0 |
0 |
0 |
| 21 |
1 |
0 |
1 |
0 |
1 |
1 |
| 22 |
1 |
0 |
1 |
1 |
0 |
1 |
| 23 |
1 |
0 |
1 |
1 |
1 |
0 |
| 24 |
1 |
1 |
0 |
0 |
0 |
0 |
| 25 |
1 |
1 |
0 |
0 |
1 |
1 |
| 26 |
1 |
1 |
0 |
1 |
0 |
1 |
| 27 |
1 |
1 |
0 |
1 |
1 |
0 |
| 28 |
1 |
1 |
1 |
0 |
0 |
1 |
| 29 |
1 |
1 |
1 |
0 |
1 |
0 |
| 30 |
1 |
1 |
1 |
1 |
0 |
0 |
| 31 |
1 |
1 |
1 |
1 |
1 |
0 |
Единичные значения данная функция будет принимать на
следующих входных наборах:
f = 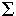 (7,11,13,14,19,21,22,25,26,28) (7,11,13,14,19,21,22,25,26,28)
Выполним минимизацию с использованием карты Карно 5-го порядка:
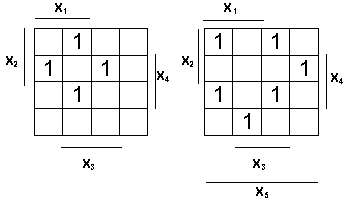
Отсюда видно, что образовать покрытия рангов менее 5-го не
удается, т.е. в данном случае СДНФ и будет МДНФ. Поэтому следует
искать скобочные разложения МДНФ с целью уменьшения числа
логических операций.

Рассмотрим сначала реализацию данной функции в базисе функции
Шеффера (2И-НЕ).
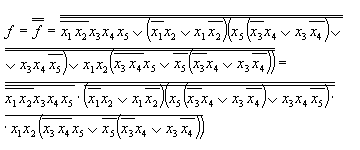
Для сокращения записи введем следующие обозначения:
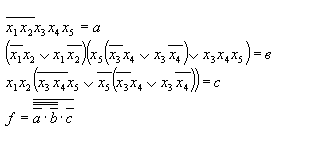
Выполнив разложения для а получим:
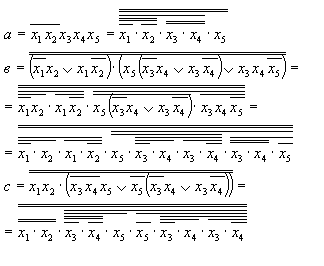
Функциональная схема примет следующий вид
(рис. 4.3.)
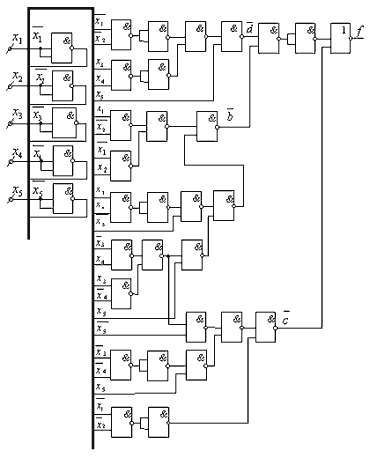
Рис. 4.3.
Получаем 34 функциональных элемента или 9 корпусов. Посмотрим,
как изменится разложение функции, если сделать его в базисе
Пирса (2ИЛИ-НЕ)
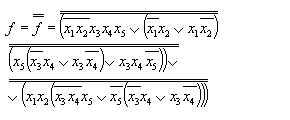
Обозначим:
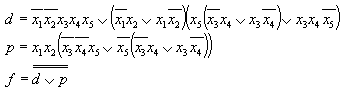
Выполняя разложение для d и p получим:
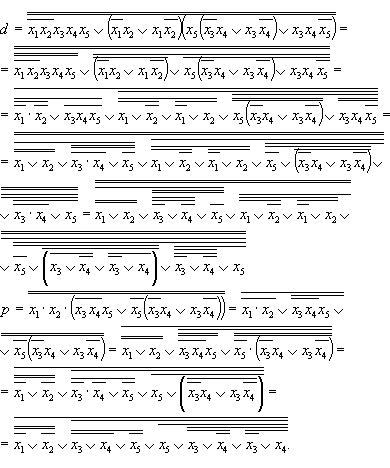
Функциональная схема в базисе Пирса принимает следующий
вид (рис. 4.4).
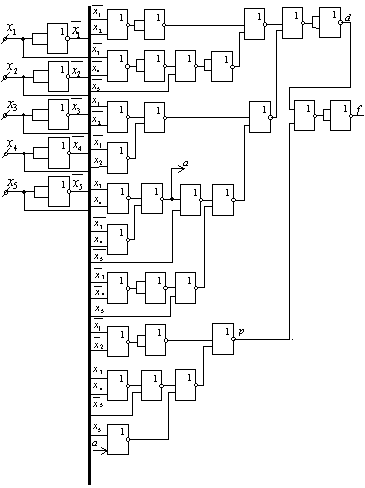
Рис. 4.4.
Получаем 35 функциональных элементов или 9 корпусов.
Можно предположить, что более экономной должна получиться
реализация в универсальном (традиционном базисе) 2И, 2ИЛИ, НЕ.
Получим следующую функциональную схему:
(рис. 4.5).
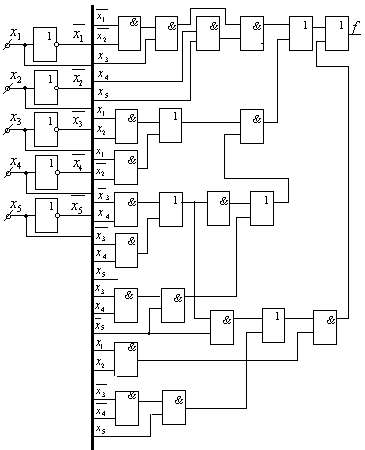
Рис. 4.5.
Получаем: 5 элементов НЕ, 17 элементов 2И, 6 элементов 2ИЛИ.
Учитывая разделение элементов по корпусам ИС имеем: 1 корпус НЕ,
5 корпусов И, 2 корпуса ИЛИ. Итого 8 корпусов.
Можно построить бесконечное число вариантов эквивалентных
функциональных схем. Такие схемы будут эквивалентны логически,
но не эквивалентны схемотехнически (по количеству функциональных
элементов, корпусов, объему и площади, энергопотреблению и т.д.).
Поэтому перед разработчиком открываются широкие возможности
поиска оптимальных вариантов в соответствии с выбранными
критериями оптимизации и собственным конструкторским и
эксплуатационным опытом.
|

