Такой метод реализации является заведомо избыточным, т.к.
функции, входящие в систему (4.4.1.) могут содержать одинаковые
ЭК или скобочные выражения. Известен метод совместной минимизации
системы БФ, который заключается в нахождении совместных
импликант и построении МДНФ системы функции через такие
импликанты. Данный метод предусматривает нахождение всех
конъюкций вида:
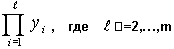
Процесс построения таких произведений
достаточно трудоемок, а результаты совместной минимизации
часто оказываются незначительными для КС средней сложности
(n = 3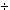 
6, m = 3
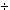6).
При n и m больших, чем 6-7 реализация метода совместной
импликации вручную становится практически невозможной. Поэтому,
с точки зрения инженерной практики, целесообразно выполнять
минимизацию функций системы (4.4.1.) по отдельности, а затем
найти или выделить совпадающие ЭК или более сходные фрагменты.
При этом открываются широкие возможности поиска оптимальных
реализаций, как и для КС с одним выходом. В качестве примера
рассмотрим табличную реализацию функции 1/sin x на интервале
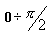дискретностью 0.1 рад.
Исходная таблица функции имеет вид (с точностью до двух
десятичных цифр):
Таблица 4.2.
| x |
1/sin x |
| 0.0 |
 |
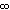| 0.1 |
10 |
| 0.2 |
5.0 |
| 0.3 |
3.4 |
| 0.4 |
2.6 |
| 0.5 |
2.1 |
| 0.6 |
1.8 |
| 0.7 |
1.6 |
| 0.8 |
1.4 |
| 0.9 |
1.3 |
| 1.0 |
1.2 |
| 1.1 |
1.1 |
| 1.2 |
1.1 |
| 1.3 |
1.0 |
| 1.4 |
1.0 |
| 1.5 |
1.0 |
И используем 4 входных разряда и 8 выходных разрядов (для
представления двух десятичных цифр). Выходная комбинация FFH
(1111 11112) будет служить признаком переполнения, т.е.
идентифицировать значение .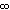
Тогда получим следующее представление функции в виде булевой
таблицы:
Таблица 4.3.
| Входные переменные |
Выходные переменные |
| x1 |
x2 |
x3 |
x4 |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
| 0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
| 0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
| 0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
| 1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
Выполняем раздельную минимизацию функций с помощью карт
Карно:
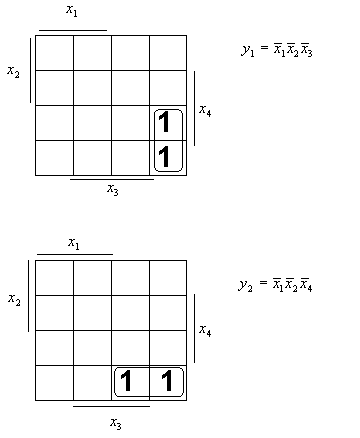
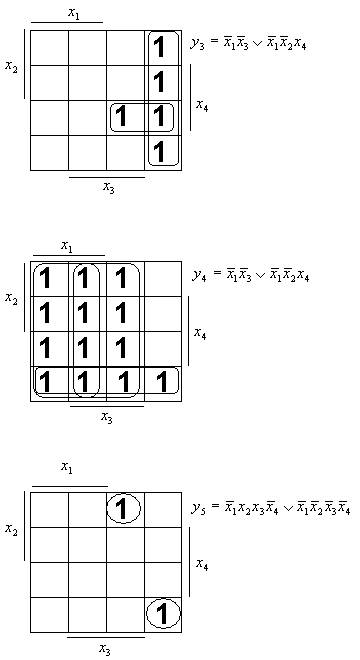
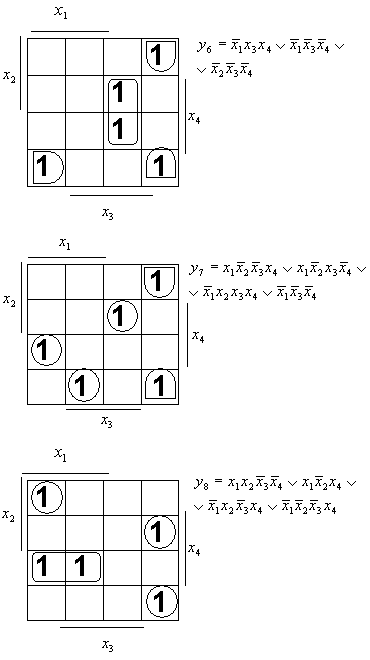
Система функций примет вид:
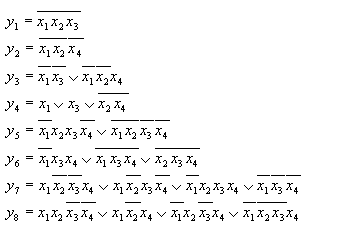
Можно выделить следующие совместные фрагменты:
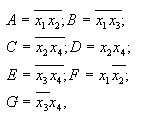
тогда получим:
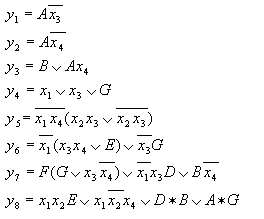
Функциональная схема в базисе 2И, 2ИЛИ, НЕ примет вид
(рис. 4.9). Эта схема содержит 4 элемента НЕ, 28 элементов 2И,
12 элементов 2ИЛИ, занимает 11 корпусов ИС и максимальная
задержка составит 6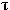
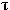(-средняя задержка распространения для
одного логического элемента).
Теперь сравним полученную реализацию со схемой, воплощающей
тривиальный способ. Для этого удобно рассмотреть базис 4И-НЕ, НЕ.
Функциональная схема в этом базисе имеет вид (рис. 4.10). Она содержит
6 элементов НЕ, 24 элемента 4И-НЕ, требует 13 корпусов ИС и имеет
задержку 3.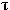
Следовательно, тривиальная схема незначительно проигрывая в
объеме, имеет существенное преимущество по быстродействию.
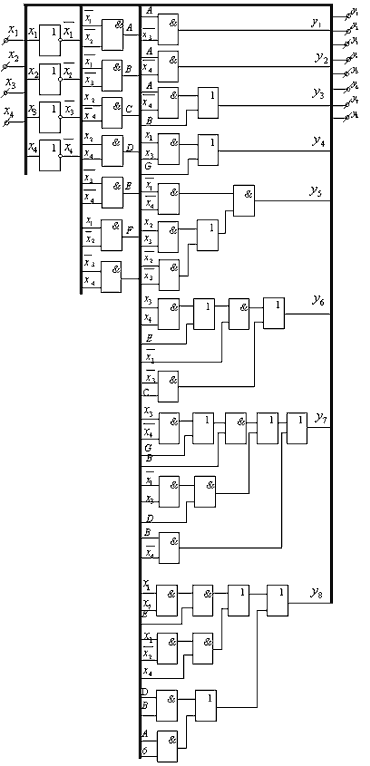
Рис. 4.9.
Рис. 4.10.
.gif){kind=spacer}
