При задании булевой функции в виде ДНФ, будет задано и множество ее еденичных значений, что будет соответствовать комбинации интервалов на пространственном кубе или комбинации покрытий на карте Карно.

Например, рассмотрим функцию трех переменных:

f (x₁,x₂,x₃) = x₁x₂ v x₁x₃ v x₁x₂x₃

ДНФ содержит три конъюнкции, которые представляются следующими интервалами (рис. 3.1.). На карте Карно получатся следующие покрытия (рис. 3.2.). Таким образом, существует взаимно однозначное соответствие между ДНФ, интервалами пространственного куба и покрытиями на карте Карно.

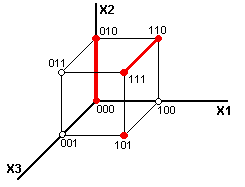
Рис. 3.1.

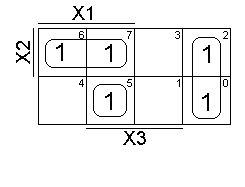
Рис. 3.2.

Задача нахождения МДНФ может быть сформулирована как задача построения такого множества покрытий единичных значений булевой функции, при котором сложность ДНФ будет минимальной.

Графически это означает, что необходимо и достаточно найти множество покрытий минимального ранга, представляющих множество единичных значений булевой функции.

МДНФ для рассматриваемой функции можно построить из трех интервалов второго ранга на пространственной решетке, что соответствует трем покрытиям 2-го ранга на карте Карно (рис.3.3., рис.3.4.).

f (x₁,x₂,x₃) = x₁x₂ v x₁x₃ v x₁x₂x₃ = x₁x₃ v x₁x₂ v x₁x₂x₃ v x₁x₂x₃ v x₁x₂x₃ = x₁x₃ v x₁x₂ v x₁x₂x₃ v x₁x₃(x₂ v x₂) = x₁x₃ v x₁x₂ v x₁x₃ = x₁x₂ v x₁x₃ v x₁x₃

f (x₁,x₂,x₃) = x₁x₂ v x₁x₃ v x₁x₃

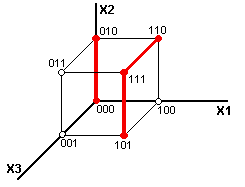
Рис. 3.3.

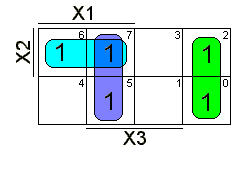
Рис. 3.4.

В правильности графического способа минимизации легко убедиться, выполнив некоторые аналитические преобразования в соответствии с законами алгебры логики.

Построение МДНФ является неоднозначным процессом, так как для данной функции может существовать несколько МДНФ, и сам процесс выбора покрытий строго не формализован.