3.1. Задачи минимизации
Задача минимизации булевых функций возникает из практических
потребностей построения логических схем, различающих аналитические
выражения булевых функций.
Как показано выше, первичной аналитической формой, получаемой
из табличного представления логической функции является СДНФ
или СКНФ. Легко понять, что в большинстве случаев значение функции
в виде СДНФ и СКНФ является заведомо не экономной, избыточной и
может быть построена эквивалентная функция, реализующая в своем
представлении меньшее число переменных и операций.
Например, обратимся к СДНФ (2.1):
f (x1,x2,x3)
= x1x2x3 v
x1x2x3 v
x1x2x3 v
x1x2x3;
Используя законы алгебры логики, получим:
f
= x1x2x3 v
x1x2x3 v
x1x2(x3x3) =
x1x2x3 v
x1x2x3 v
x1x2.
Простейшее или минимальное в некотором смысле представление
булевой функции необходимо искать в некотором определённом базисе.
Наилучшие результаты получены для базиса, включаюшего инверсию,
дизъюкцию и коньюкцию. Поэтому в дальнейшем задача минимизации
будет рассматриваться именно в этом базисе.
В соответствии с введённым в разделе 2.3 определением под
сложностью нормальной формы следует
понимать сумму рангов её составляющих, т.е. число букв в ней.
Поэтому ДНФ, имеющая наименьшую сумму рангов среди всех ДНФ,
эквивалентных данной функции, называется минимальной ДНФ (МДНФ). Если же в качестве
меры сложности рассматривать число элементарных коньюкций в ДНФ
или число элементарных дизъюкций в КНФ, то ДНФ, имеющая наименьшую
длину среди всех ДНФ, эквивалентных данной функции называется
кратчайшей ДНФ (КДНФ).
Построение кратчайших и минимальных ДНФ имеет свою специфику.
КДНФ и МДНФ могут находиться в разных теоретико-множественных отношениях:
множества КДНФ и МДНФ содержаться одно в другом или иметь пустое
пересечение.
Если к исходной ДНФ применять лишь операции склеивания AB v AB = A
и поглощения AB v A = A,
то рано или поздно дальнейшие преобразования окажутся невозможными. В
этом случае будет получаться тупиковая ДНФ,
т.е. такая ДНФ, при удалении из которой любой коньюкции, полученная в
результате ДНФ не будет эквивалентна исходной.
Среди множеств, ТДНФ должны содержаться и МДНФ. Поэтому теоретически
можно искать МДНФ, сравнивая показания ТДНФ путём последовательного
перебора. Оценка числа тупиковых ДНФ дана И.Ю. Журавлёвым. Для
достаточно больших n число ТДНФ оценивается как
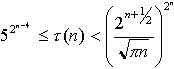
Поэтому уже для n > 10 процесс перебора оказывается длительным и
практически не применяется даже с помощью ЭВМ.
Ю.Л. Васильев показал, что существуют такие булевые функции, зависящие
от n аргументов, для которых ТДНФ может быть в 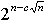 раз сложнее МДНФ, где С – некоторая
константа. Поэтому для таких функций поиск ТДНФ недаёт удовлетворительрого
результата.
Получены важные оценки и для КДНФ. И.Ю. Журавлёв установил,
что среди КДНФ может и не содержаться МДНФ и для достаточно больших n
сушествуют такие булевы функции, для которых КДНФ содержит на
2n-12 букв больше, чем МДНФ этой же функции.
Результаты А.Д. Коршунова показывают, что почти для всех функций
алгебры логики КДНФ и ТДНФ не совпадают.
И.С. Потёмкин предложил разделять логические функции на три группы!
- функции малого числа аргументов;
- "объективные" функции многих аргумментов;
- "субъективные" функции многих аргументов.
К первой группе относят функции 3 – 5 аргументов,
которые весьма часто встречаются при реализации цифровой
аппаратуры. Для таких функций минимизация не представляет
серьёзных проблем.
Ко второй группе относятся функции более чем пяти
аргументов, которая отражает некоторые естественные,
технические или природные зависимости (таблицы дискретизации
некоторых функций, таблицы попраиочных коэффициентовдатчиков
и т.п.). Большинство из таких функций оказывается неминимиризируемыми.
Поэтому для их реализации используются специальные схемы ПЛМ и
ПЗУ, которые рассматриваются в главе 5.
Третью группу составляют функции большого числа аргументов,
составленные человеком. Для этих функций, как правило, характерно
наличие внутренней структуры и, следовательно, возможностей
декомпозиции на более простые позиции.
Разработанные методы минимизации достаточно хорошо работают
для функций первой и третьей группы и не дают гарантированного
результата для функций втрой группы.
Современная элементная база интегральных микросхем позволяет
выбрать такие функциональные элементы для построения логических
схем, которые требуют незначительной миримизации и преобразования
исходных СДНФ или СКНФ, или же совсем не требуют минимизации.
В дальнейшем, под задачей минимизации булевых функций будем
понимать задачу нахождения МДНФ или МКНФ.
|
.gif){kind=spacer}
