.gif) |
2.3. Графическое представление булевой функции. Карты карно
Из инженерной и математической практики хорошо известно, что
графическое представление математических объектов является наиболее
наглядным и удобным для конструктивного использования. Поэтому
широкое применение находит представление булевых функций с помощью
пространственных двоичных решёток.
Поскольку одна булева переменная может принимать два значения
"0" и "1", то её можно интерпретировать отрезком прямой (рис. 2.1а),
являющимся одномерным пространством.
Рис. 2.1.а
От одной переменной может быть построено четыре функции в
алгебре логики (табл. 1.1). Их можно представить на этом
отрезке, показывая нулевое значение функции как "0", а единичное
- как "1" (рис.2.1 б).
Рис. 2.1.б
Для двух и трех переменных мы получим квадрат на плоскости и
куб в трёхмерном пространстве соответственно (рис. 2.1 в и г).
Рис. 2.1.в
Рис. 2.1.г
Для нашего примера:
f (X1,X2,X3) =
X1· X2· X3v
X1· X2· X3v
X1· X2· X3v
X1· X2· X3
В дальнейшем знаки конъюнкции ( · ) будем опускать, т.е.
X1· X2·
X3  X1X2X3
X1X2X3
Также показано, что любая таблично заданная функция
алгебры логики может быть представлена в форме:
Фi(X1,
X2, ..., Xn) = Фi1·
Фi2· ... Фik =
&Фij, ij  Т0, Т0,
где Фi(X1, X2, ...,
Xn) - характеристическая функция нуля,
определённая как:
Фi = {0;1}
0 – если номер набора есть i,
1 – в противном случае.
Т0 – есть множество наборов, из которых
функция обращается в ноль.
Нормальные формы булевых функций
Произведение
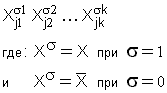
называется элементарной конъюнкцией
ранга k, если все переменные в нем различны. Логическая единица считается
элементарной конъюнкцией ранга 0.
Логическая сумма
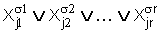
называется элементарной дизъюнкцией
ранга r, если все переменные в ней различны. Логический ноль считается
элементарной дизъюнкцией ранга 0.
Формула вида
u1 v u2
v ... v ui
где: u1, u2, ... ui – различные элементарные
конъюнкции рангов r1, r2, ... ri соответственно называется
дизъюнктивной нормальной формой
(ДНФ), а число 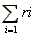 – сложностью ДНФ.
– сложностью ДНФ.
Формула вида
S1· S2·
... · St
где: S1, S2, ... St –
различные элементарные дизъюнкции рангов p1,
p2, ... pt соответственно
называется конъюнктивной нормальной формой
(КНФ), а число 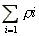 – сложностью КНФ. – сложностью КНФ.
Всякая булева функция, отличная от тождественного "0"
может быть задана ДНФ и, в общем случае, неоднозначно.
Аналогичное правило действует и для КНФ, если булева функция
не тождественна "1".
По таблице задающей булеву функцию f
(Х1, Х2, ... Хn) строится
совершенная ДНФ:
u1 v u2
v ... v uS,
где 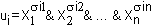 таковы, что i = 1, 2, ..., S и наборы
таковы, что i = 1, 2, ..., S и наборы  i1, i1,
 i2, ..., i2, ...,  in
таковы, что f ( in
таковы, что f ( i1, i1,
 i2, ..., i2, ...,  in)
= 1. in)
= 1.
Совершенная КНФ имеет вид:
S1 & S2
& ... & SC
где 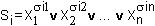 таковы, что i = 1, 2, ..., S и наборы
таковы, что i = 1, 2, ..., S и наборы  i1, i1,
 i2, ..., i2, ...,  in
таковы, что f ( in
таковы, что f ( i1, i1,
 i2, ..., i2, ...,  in)
= 0. in)
= 0.
Совершенная ДНФ и КНФ для заданной булевой функции
строятся однозначно. Они четко получаются из таблицы
истинности булевой функции следующим образом.
Для СДНФ:
- необходимо выбрать из таблицы истинности функции все
наборы аргументов, на которых функция принимает значения
"1";
- выписать элементарные конъюнкции, соответствующие
этим наборам элементов; если Хi входит в
данный набор как 1, он вписывается без изменения в
конъюнкцию, если Хi входит в данный набор
как 0, то в конъюнкции вписывается отрицание Хi
(т.е. Xi);
- все полученные элементарные конъюнкции соединяются
между собой знаками дизъюнкции (т.е. v).
Для СКНФ:
- необходимо выбрать в таблице истинности функции все
наборы аргументов, на которых функция принимает значения "0";
- выписать элементарные дизъюнкции, соответствующие этим
наборам элементов; если Xi входит в данный набор
как 0, он вписывается без изменений в дизъюнкцию, если
Xi входит в данный набор как 1, то в дизъюнкцию
вписывается его отрицание (т.е. Xi);
- все полученные элементарные дизъюнкции соединяются между
собой знаками конъюкции (т.е. · ).
В случае нашего примера СДНФ представленой формулой (2.1),
а СКНФ - формулой (2.2).
|

