.gif) |
2.2. Аналитическое представление булевой функции.
Нормальные формы
Рассмотрим булеву функцию f
(X1, X2, ..., Xn); каждому набору
входных переменных (X1, X2, ..., Xn)
можно сопоставить двоичное число вида:
i = X1· 2n-1 +
X2· 2n-2 + ... +
Xn· 20.
Можно ввести функцию Fi(X1,
X2, ..., Xn) следующим образом:
Fi = {0;1},
1 – если номер набора есть;
0 – в противном случае.
Тогда заданную функцией алгебры логики можно представить в форме:
Fi(X1,
X2, ..., Xn) = Fi1 v
Fi2 v ... v Fik = v
Fij, ij  Т, Т,
где Т есть
множество наборов, на которых функция принимает истинное
значение ("1"), (15).
В инженерной практике номера наборов i записывают десятичными
числами и функцию задают в виде:
F = v (j1, j2, ..., jn)
= 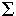 (j1, j2, ..., jn) (j1, j2, ..., jn)
Для примера табл. 2.1 получим:
F(X1, X2, ..., Xn) =
1011 v 1101 v 1110
v 1111
F = v (3, 5, 6, 7) = 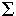 (3, 5, 6, 7) (3, 5, 6, 7)
Множество Т = (3, 5, 6, 7)
Доказано, что функцию Fi можно представить как
конъюнкцию аргументов (X1, X2, ...,
Xn), такую, что если Xi в наборе
(X1, X2, ..., Xn) равен 0,
то в конъюнкцию входит инверсия Xi (т.е.
Xi), если Xi
равен 1, то в конъюнкцию входит Xi.
|

