3.4. Метод Квайна-Мак'Класки

Основным недостатком метода Квайна является необходимость полного по парного сравнения ЭК на этапе нахождения первичных импликант. Поэтому при большом числе ЭК применение метода Квайна становится весьма затруднительным.

Мак-Класки (Mc Cluskey E.) предложил модернизацию алгоритма Квайна, которая заключается в том, что все ЭК, входящие в СДНФ записывается в виде двоичных чисел (номеров наборов), которые группируются по числу входящих в них единиц в непересекающиеся классы. В класс с номером i войдут все ЭК содержащие в своей двоичной записи i единиц. По парное сравнение следует производить между соседними по номеру классами, так как только в них могут находиться склеивающиеся ЭК.

При образовании ЭК ранга меньше n вместо исключенных переменных ставится символ стирания x.

ЭТАП 1. Нахождение первичных импликант.

Продолжаем рассматривать пример раздела 3.3.

Исходная функция

f = 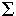(1, 3, 7, 8, 11, 12, 13, 18, 19, 24, 25, 26, 27)

Разбивая ЭК на классы по числу единиц, получим:

К₁ = (00001*, 01000*);
К₂ = (00011*, 10010*, 11000*, 01100*);
К₃ = (00111*, 01011*, 01101*, 10011*, 11001*, 11010*);
К₄ = (11011*).

Образуем новые классы путем склеивания ЭК в соседних классах К₁...К₄:

К₁^* = (000x1, x1000, 01x00*);
К₂^* = (00x11, 0x011*, x0011*, 1001x*, 1x010*, 1100x*, 110x0*, 0110x);
К₃^* = (x1011*, 1x011*, 110x1*, 1101x*).

Строим ЭК 3-го ранга:

К₁^** = (000x1, x1000, 01x00);
К₂^** = (00x11, xx011, 1x01x, 110xx, 0110x).

Дальнейшие склеивания не возможны, поэтому переходим ко второму этапу (табл. 3.3.).

После вычеркивания избыточных столбцов и избыточных первичных импликант получим следующую таблицу (табл. 3.4.).

Полученная МДНФ примет вид:
000x1, 01x00, 00x11, xx011, 1x01x, 110xx, 0110x.

Нетрудно убедиться, что МДНФ, полученная двумя методами совпадают.

Таблица 3.3.

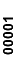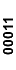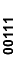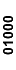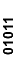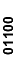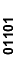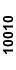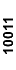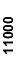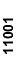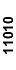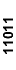000x1

x1000

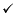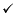01x00

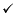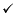00x11

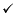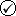xx011

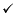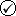1x01x

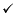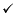110xx

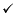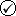0110x

Таблица 3.4.

x1000
01x00