.gif) |
5.3. Мультиплексоры
Мультиплексором называется такой функциональный цифровой
элемент, который имеет к- адресных (или селекторных) входов,
2к - информационных входов (входов данных), вход разрешения и
обязательно прямой, а возможно и инверсный выход. Условное
изображение мультиплексора имеет вид, представленный на
рис. 5.13.
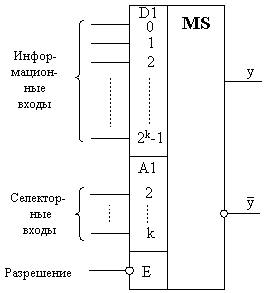
Рис. 5.13.
Мультиплексор подключает к выходу тот информационный вход,
номер которого задается кодовой комбинацией (двоичным номером)
на селекторных входах. Поэтому кратко мультиплексоры обозначают
как 2*1, 4*1, 8*1 и т.д.
Обозначение MS можно расшифровать как multiselector.
В настоящее время число информационных входов мультиплексоров
обычно ограничивается восемью (серии КР1533, КР1554).
Мультиплексоры как функциональные элементы являются удобным
базисом для реализации логических функций. В зависимости от
числа входных переменных БФ-й, и параметра мультиплексора k,
возникает несколько методов построения КС на мультиплексорах.
Метод 1. Число входных переменных ЛФ равно числу
селекторных входов (n = k). В этом случае реализуется
тривиальный метод проектирования, заключающийся в том, что
входные переменные нужно подключить к селекторным входам,
в соответствии с их весами, а на информационные входы подать
логические нули и единицы в соответствии с таблицей
истинности ЛФ.
Например, имеется логическая функция трех переменных
f =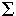 
(0,1,2,4,5). Для ее реализации можно использовать
мультиплексор КР1533КП7 и построить следующую схему
рис. 5.14.
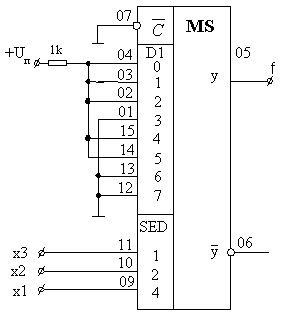
Рис. 5.14.
Информационные входы с номерами 0,1,2,4,5, соответствующие
единичным значениям функции подключаются к высокому уровню,
а входы с номерами 3,6,7, соответствующие нулевым значениям
функции - к низкому уровню. Считает, что входная переменная
х1 является старшим (крайним левым) разрядом в коде
входного набора.
Схемотехнически данные ИС устроены так, что при высоком
уровне на входе C выход Y
устанавливается в логический "0" (низкий уровень, а выход y -
в логическую "1" (высокий уровень).
Внимательный читатель легко оценит достоинства приведенной
схемы: не требуется выполнять минимизацию ЛФ, практически
отсутствует этап разложения ЛФ по элементарному базису,
реализация строится непосредственно по таблице БФ. Но такие
простые решения возможны в инженерной практике далеко не
всегда. Поэтому переходим к следующему методу.
Метод 2. Число входных переменных логической функции
на единицу больше числа селекторных входов (n = k + 1).
В этом случае одну из входных переменных следует "вынести" на
информационные входы, т.е. представить ЛФ в виде:
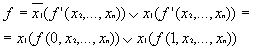
Функции f
(0, х1, ..., хn) и
f (1, х1, ..., хn)
являются функциями от n-1 аргумента, что в нашем случае равно
k, и могут быть представлены в виде СДНФ:
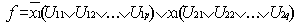
где Uij есть ЭК ранга n-1.
Это представление исходной функции f
можно интерпретировать таким образом: двоичные коды,
соответствующие ЭК ранга n-1 определяют номера информационных
входов, на которые следует подать X1
и Х1 соответственно. В случае, если U1i = U2j,
то U1i(x1 v x1) = 1,
следовательно на этот вход следует подать логическую "1".
Продемонстрируем этот метод на примере функции
f =
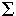(3, 5, 6, 7, 14, 15). СДНФ принимает
вид:
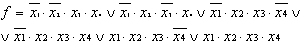
Выполняем разложение:
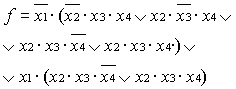
Если перейти к двоичной записи, то
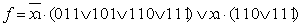
Следовательно, на информационные входы 3 и 5 следует подать
переменную X1, на входы 6 и 7
логическую единицу. Соответствующая схема представлена на
рис. 5.15.
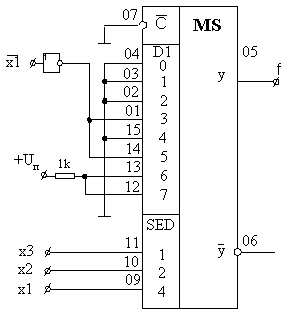
Рис. 5.15.
В случае n = k + 1 возможно использование двух мультиплексоров,
один из которых должен включаться при Х1=0, а другой при Х1=1,
и выходы этих мультиплексоров следует объединить по ИЛИ.
Очевидно, что для примера рассмотренного выше (рис. 5.15.)
такое решение является заведомо избыточным, но применение двух
мультиплексоров возможно в случае использования сдвоенных ИС
типа КР1533КП2. Для функции f =
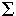(0, 1, 2, 4, 5) (рис. 5.15.) такое
решение примет следующий вид (рис. 5.16.):
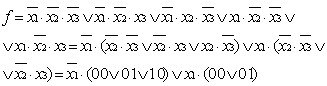
Рис. 5.16.
Метод 3. Число входных переменных ЛФ на два и более
превосходит число селекторных входов (n >= k+2). Возможно
вынесение избыточных переменных на селекторные входы с
использованием одного мультиплексора, а также вынесение
переменных с использованием числа мультиплексоров, равного
степени двух. Проанализируем это на следующих примерах:
требуется реализовать функцию пяти переменных
f =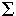
(1, 2, 3, 6, 7, 9, 11, 15, 16, 20, 21, 25). Выполняя разложение
получим:
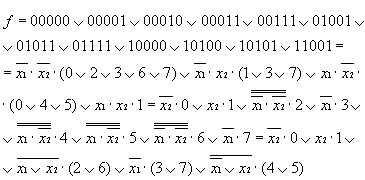
Как видно из последней записи, для реализации данной схемы
достаточно одного мультиплексора с тремя селекторными входами
и четырех элементов 2ИЛИ-НЕ, на двух из которых реализованы
инверторы.
Чертеж соответствующей схемы приведен на рис. 5.17.
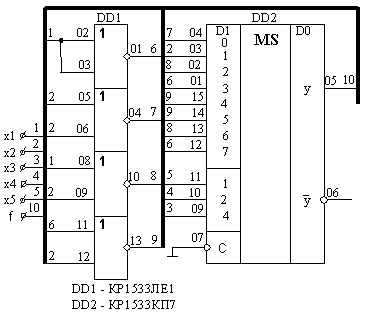
Рис. 5.17.
При использовании же схемы КР 1533КП2 разложение следует
продолжить:
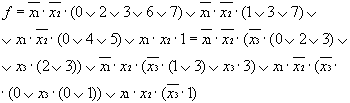
Схема принимает вид, представленный на рис. 5.18.
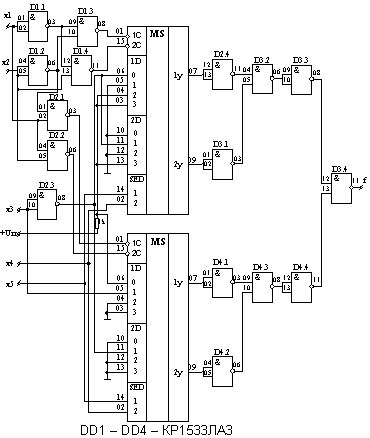
Рис. 5.18.
Очевидно, что данная схема весьма нерациональна по значению
временной задержки, поэтому можно предложить вариант с
использование дешифратора рис. 5.19.
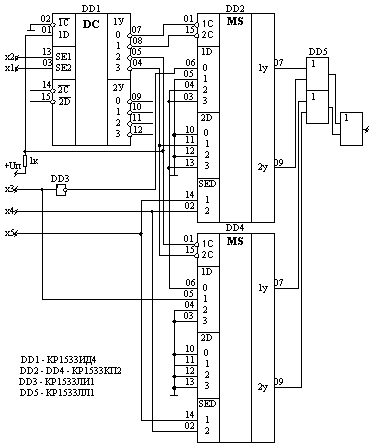
Рис. 5.19.
|
